MD-Blog_Web Creative

頭の体操

今年も師走になり、バタバタしているところでしょうが、、、
ということで、帰ってきた2年ぶりの算数ドリルで頭の体操をしましょう。
前回sinとcosを使ってみたので、今回はtanを使ってアニメーション制作によく使うであろうTipsをご紹介します。

概要

ランダムな2点間の距離を求めるのに必要なのは、みんな大好き「三平方の定理」です。

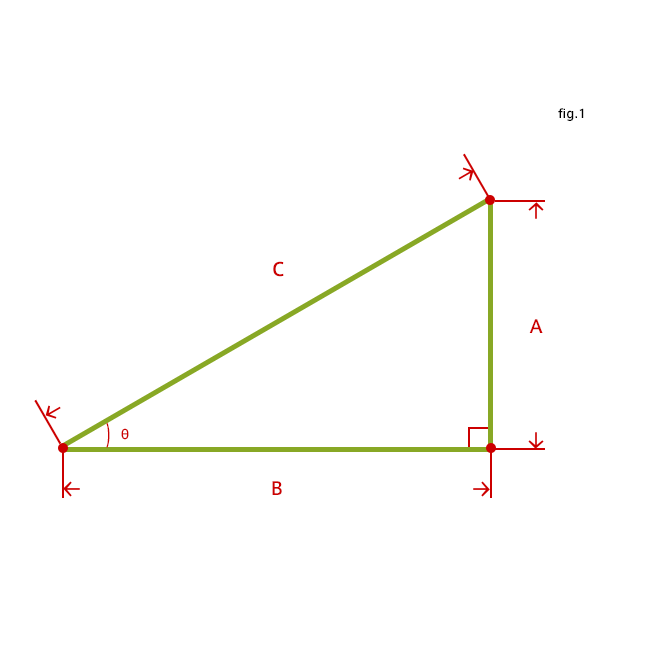
直角三角形において斜辺の長さをC、直角と隣り合う2辺の長さをA,Bとするとき
A x A + B x B = C x C
が成立する。（※fig1）

というやつですね。

またランダムな2点間を結ぶ直線の角度を求めるのに必要なのは、タンジェント（正接）を使います。
この時点で「？？？」となっているアナタ。
上図（※fig1）の三角形でいうと、
tanθ = A / B
となります。※θは角度（ラジアン）

なので、知りたい角度は、
θ　= arctan(A / B)
となります。

arctan？？？
「アークタンジェント」と読みます。
arctanはtanの逆関数なのですが、逆関数？となると思うので、以下が成り立つと思ってもらえればわかりやすいかと思います。
tanX = Y
X = arctanY
なので、要はtanθのθを知りたいので使っています。

お題

今回はその任意の2点の距離と角度を使って、

• 最初にクリック（タップ）した点と、次にクリック（タップ）した点を結ぶラインを引く
• ラインを引くのにかかる時間は、2点間の距離に応じて計算する

ということをやってみたいと思います。

まずはデモを開き、どこか任意の違う場所を2か所クリック（タップ）してみてください。
※動作確認 PC：Chrome, Firefox、SP：Android Chrome

解説

実装に関しては上記の決まり事（公式）を当てはめるだけなので難しいことはないので、みなさんお好きな方法で実装していただければと思いますが、ここでは僕の実装例をご紹介したいと思います。

実装することは、

• クリック（タップ）された2点を取得する
• 2点間の距離と角度を求める

になります。

シンプルですね。

では実際に上記をJSで書いていきます。（※デモよりわかりやすくシンプルにしてます。）

クリック（タップ）された2点を取得する

/**
 * 各パラメータ
 */
var hasStart = false; //クリック（タップ）1回目：false, 2回目：true
var startPointX = 0;    //クリック（タップ）1回目のx座標
var startPointY = 0;    //クリック（タップ）1回目のy座標
var endPointX = 0;    //クリック（タップ）2回目のx座標
var endPointY = 0;    //クリック（タップ）2回目のy座標

/**
 * リスナー作成
 */
window.document.getElementById("data-evt").addEventListener("click",onClickHandler);    //#data-evtはイベント取得用のDOM

/**
 * クリック（タップ）された点を取得する
 * @param e MouseEvent
 */
function onClickHandler(e){
    console.log("x, y : " + e.clientX + ", " + e.clientY);
    if(!hasStart){
        //1回目のクリック（タップ）
        startPointX = e.clientX;
        startPointY = e.clientY;
    }else{
        //2回目のクリック（タップ）
        endPointX = e.clientX;
        endPointY = e.clientY;
    }
    hasStart = !hasStart;
}

ここは単純に、

• マウスクリック（タップ）されたときの関数を登録
• マウスクリック（タップ）されたら、
  • 1回目か2回目か判断
  • クリック（タップ）された点の座標（X,Y）を取得・格納

という流れになります。

2点間の距離と角度を求める

//距離
var len = Math.sqrt(Math.pow(startPointX - endPointX, 2) + Math.pow(endPointY - startPointY, 2));
//角度
var rad = Math.atan2(endPointY - startPointY, endPointX - startPointX);

Math.sqrtは、平方根ってやつですね。
B = A x A
のとき、
A = Math.sqrt(B)
となる例のアレです。

Math.powは累乗した値を返し、
B = A x A = Math.pow(A, 2)

Math.atan2は、上記でも使用しているアークタンジェントなのですが、Math.atanとMath.atan2があり、同じことをやっているのですが、渡す引数が違います。

上図（※fig1）の三角形でいうと、
Θ = Math.atan(A / B) //比率を引数
Θ = Math.atan2(A, B) //長さを引数

内容的には「概要」にある公式を当てはめただけです。

さらにデモでは

• 線（矩形）を作成のタイミングで、scale（0→1）のアニメーション
• 2点間の距離に応じてアニメーション時間をセットする
• scaleアニメーションが終わったらalpha（1→0）のアニメーション
• alphaアニメーションが終わったらvisibleをfalseにする

を追加してます。

どうでしょうか。
インタラクティブな演出にはこのような算数が使われていることが多々ありますので、いいライブラリを探すのもいいですが、たまにはこのように根本的なところに目を向けるのも一興かと思います。
少しでも食わず嫌いが直ることを祈って！

おまけ

上記では、

• 直角三角形において2辺から最後の1辺を求める
• 任意の2点の角度を求める

ことをやっているのですが、
他にも「余弦定理」というものを使えば、直角三角形でない普通の三角形でも、

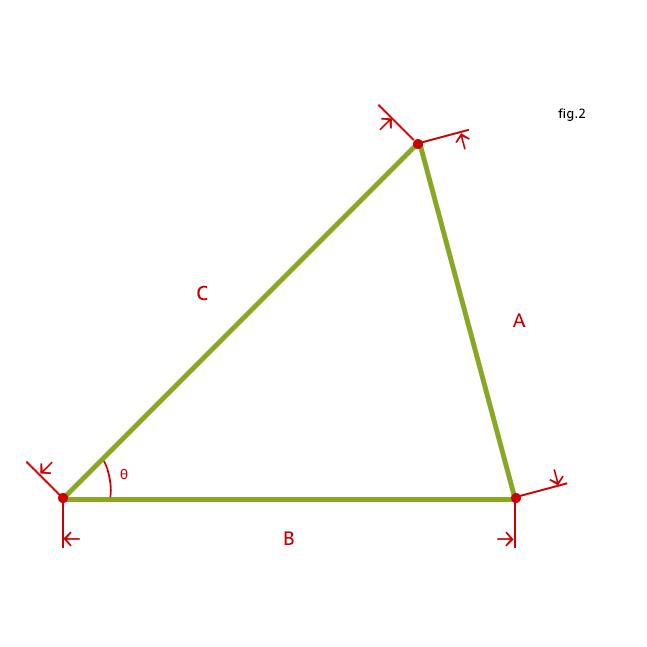
2辺と間の角度1つから残りの1辺を求める

A x A = B x B + C x C - 2 x B x C x cosθ

3辺の長さから角度3つを求める

θ = acos((B x B + C x C - A x A) / (2 x B x C))
※acos：アークコサイン
ということもできます。
興味ある方はGoogle先生に詳しく聞いてみてください。

算数ドリルシリーズ

• 算数ドリル ... 動的レイアウトを考えよう
• 算数ドリル ... 三角関数sin/cosの基本
• 算数ドリル ... 二点間の距離と角度